Particles#
Generating Particles from ClusterModel Objects#
Once a ClusterModel object is created,
it can be used to generate particle positions and velocities, of gas, dark matter,
and/or star types. The positions are generated by drawing uniform random numbers
\(u \in [0, 1]\), and inverting the equation \(u = M(<r)/M_{\rm tot}\)
to find the radius \(r\). Since the cluster is spherically symmetric, the
particle positions are isotropically distributed in the tangential directions
\(\theta\) and \(\phi\). Masses are also assigned to the particles based
on the number of particles and the total mass of the gas, dark matter, or stars.
These fields are named "particle_position", "particle_velocity", and
"particle_mass". The first two have shapes of (number_of_particles, 3)
(containing all three components of each), and the latter has a shape of
number_of_particles.
Gas Particles#
Gas particles are initialized in hydrostatic equilibrium from the profiles. In
addition to the fields mentioned above, gas particles also have "density",
and "thermal_energy" fields. They may optionally also have a
"magnetic_field" field, which is a vector field with shape
(number_of_particles, 3). This field is not derived from hydrostatic
equilibrium and thus needs to be set later by the user, either by hand or
from a 3D field. See Mapping a Field to Particles for details.
To generate gas particles, use the
If you want to add a field with the particle gravitational
potential, set compute_potential=True. If you want to limit the
generation of particles to within a certain radius, set r_max equal to
the desired radius in kpc (otherwise the maximum radius will be the value
which was originally supplied in the creation of the
ClusterModel object):
n_gas = 1000000 # number of particles to generate (now within r_max)
r_max = 5000.0 # maximum radius of particles in kpc
gas_particles = p.generate_gas_particles(n_gas, r_max=r_max,
compute_potential=True)
Dark Matter and Star Particles#
Dark matter and star particles are initialized with velocities assuming collisionless dynamics and virial equilibrium with the underlying gravitational potential from all mass sources.
Virial Equilibria: Mathematical Overview#
The mass density \(\rho({\bf r})\) of such a system can be derived by integrating the phase-space distribution function \(f({\bf r}, {\bf v})\) over velocity space:
where \({\bf r}\) and \({\bf v}\) are the position and velocity vectors. Assuming spherical symmetry and isotropy, all quantities are simply functions of the scalars \(r\) and \(v\), and \(d^3{\bf v} = 4\pi{v^2}dv\):
Assuming zero net angular momentum for the cluster, there is a unique distribution function \(f(E)\) which corresponds to the density \(\rho(r)\). Since the total energy of a particle is \(E = v^2/2 + \Phi\) (where \(\Phi(r)\) is the gravitational potential) and further defining \(\Psi = -\Phi\) and \({\cal E} = -E = \Psi - \frac{1}{2}v^2\), we find:
After differentiating this equation once with respect to \(\Psi\) and inverting the resulting Abel integrel equation, we finally have:
which given a density-potential pair for an equilibrium halo, can be used to determine particle speeds. For our cluster models, this equation must (in general) be solved numerically, even if the underlying dark matter, stellar, and gas densities can be expressed analytically.
To generate the particle speeds, the distribution function \(f({\cal E})\) is used with uniform random numbers \(u \in [0, 1]\) via an acceptance-rejection method. The particle velocity components are isotropically distributed in the tangential directions \(\theta\) and \(\phi\).
Checking the Virial Equilibrium#
It is probably a good idea to check that the resulting distribution functions
for the dark matter and/or stars are consistent with the input mass density
profiles. The check_dm_virial()
or check_star_virial()
methods can be used to perform a quick check on the accuracy of the virial
equilibrium model for each of these types. These methods return two NumPy
arrays, the first being the density profile computed from integrating the
distribution function, and the second being the relative difference between
the input density profile and the one calculated using this method.
import matplotlib.pyplot as plt
rho, diff = p.check_dm_virial()
# Plot this up
fig, ax = plt.subplots(figsize=(10,10))
ax.loglog(vir["radius"], vir["dark_matter_density"], 'x',
label="Input mass density", markersize=10)
ax.loglog(vir["radius"], rho, label="Derived mass density", lw=3)
ax.legend()
ax.set_xlabel("r (kpc)")
ax.set_ylabel("$\mathrm{\\rho\ (M_\odot\ kpc^{-3})}$")
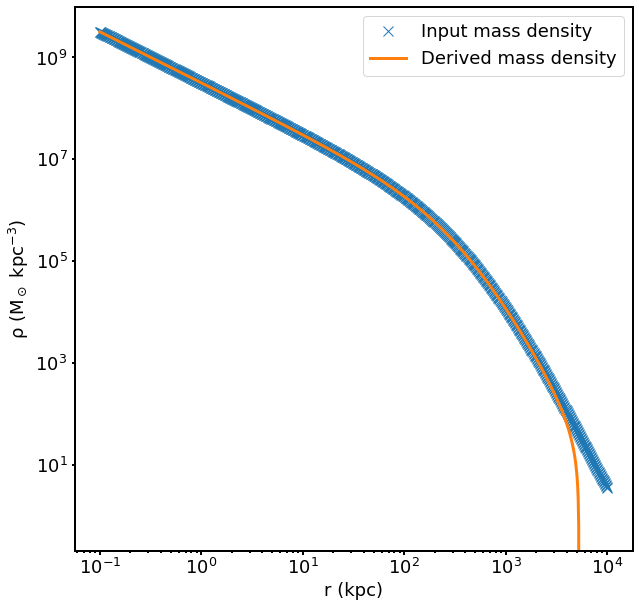
One can see that the derived density diverges from the input density at large radii, due to difficulties with numerically integrating to infinite radius. So long as the maximum radius of the profile is very large, this should not matter very much.
Generating Dark Matter and Star Particles#
The generate_dm_particles()
and generate_star_particles()
methods carry out these functions for dark matter and stars respectively, and
also assigns particle masses, given the number of particles one wishes to be
generated:
n_dm = 1000000 # number of DM particles to generate
n_star = 10000 # number of star particles to generate
dm_particles = p.generate_dm_particles(n_dm)
star_particles = p.generate_star_particles(n_star)
If you want to add a field with the particle gravitational
potential, set compute_potential=True. If you want to limit the
generation of particles to within a certain radius, set r_max equal to
the desired radius in kpc (otherwise the maximum radius will be the value
which was originally supplied in the creation of the
ClusterModel object):
n_dm = 1000000 # number of particles to generate (now within r_max)
r_max = 5000.0 # maximum radius of particles in kpc
dm_particles = p.generate_dm_particles(n_dm, r_max=r_max,
compute_potential=True)
The object returned in any of these cases is
a ClusterParticles object,
which is covered in more detail next.
The ClusterParticles Class#
The ClusterParticles class is a
container for particle properties. It is the format that is returned
from the various generate_*_particles methods described above. This
class can be used to perform further operations on particles or write
them to disk.
ClusterParticles Operations#
Several kinds of operations can be performed on
ClusterParticles objects.
Adding ClusterParticles Objects#
ClusterParticles objects can be added
together. In this case, we add particles of different types so that they
are combined into a single object:
all_particles = gas_particles+dm_particles+star_particles
If you have multiple ClusterParticles
objects with the same particle types, the particle field arrays will simply
be concatenated together:
gas_parts = gas_parts1+gas_parts2
Dropping Particle Types#
To drop all fields of a specific particle type from a
ClusterParticles instance, use the
drop_ptypes() method:
# Drop gas particles
parts.drop_ptypes("gas")
# Drop DM and star particles
parts.drop_ptypes(["dm", "star"])
Add Position and Velocity Offsets#
By default, a ClusterParticles object is
centered at (0, 0, 0) kpc and has a bulk velocity of (0, 0, 0) kpc/Myr.
To translate the particle positions of a
ClusterParticles instance to a new center,
or to boost the particle velocities to a new frame, or both, we can use the
add_offsets() method:
# shift the particle positions by this amount in each direction
r_ctr = [1000.0, -1000.0, 10.0] # kpc
# shift the particle velocities by this amount in each direction
v_ctr = [-500.0, 200.0, 0.0] # kpc/Myr
parts.add_offsets(r_ctr, v_ctr)
Note
The add_offsets() does
exactly as it is named, it adds offsets to the positions and velocities,
so these are relative translations by the given amounts and not movements
to the values of the r_ctr and v_ctr parameters.
Make a Cut on Radius#
To cut out particles beyond a certain radius, use the
make_radial_cut() method:
# make a radial cut at r_max, assuming the center is [0, 0, 0] kpc
r_max = 5000.0 # in kpc
parts.make_radial_cut(r_max)
# make a radial cut at r_max, assuming the center is
# [500, 500, 500] kpc
r_max = 5000.0 # in kpc
center = [500, 500, 500] # in kpc
parts.make_radial_cut(r_max, center=center)
You can also cut out only certain particle types:
# make radial cut on stars only
r_max = 5000.0 # in kpc
parts.make_radial_cut(r_max, ptypes="star")
# make radial cut on stars and dm
r_max = 5000.0 # in kpc
parts.make_radial_cut(r_max, ptypes=["star","dm"])
Add Black Hole Particles#
To add a single black hole particle, use the
add_black_hole()
method. The simplest way to do this is to simply provide it with a
mass, which will place a black hole particle at [0.0, 0.0, 0.0] kpc
with zero velocity:
Mbh = 3.0e9 # assumed units of Msun
parts.add_black_hole(Mbh)
to supply an alternate position and velocity, use pos and vel:
Mbh = 3.0e9 # assumed units of Msun
pos = [300.0, 100.0, -100.0] # assumed units of kpc
vel = [-200.0, -100.0, 50.0] # assumed units of kpc/Myr
parts.add_black_hole(Mbh, pos=pos, vel=vel)
to choose the position and velocity of the DM particle with the minimum
gravitational potential, set use_pot_min=True:
Mbh = 3.0e9 # assumed units of Msun
parts.add_black_hole(Mbh, use_pot_min=True)
Add a New Field or Change a Field#
A new field can be added to the particles rather easily. For example, if you wanted to add a field which added a tag to the DM particles to keep track of which halo they originated from:
num_particles1 = 1_000_000
num_particles2 = 200_000
halo1 = np.ones(num_particles1)
halo2 = 2.0*np.ones(num_particles2)
cluster1.set_field("dm", "tag", halo1)
cluster2.set_field("dm", "tag", halo2)
If you pick a field that already exists, it will be overwritten by default
with the new values, but you will get a warning. If you want to add the numerical
values to those of the existing field, set add=True:
import unyt as u
B0 = 1.5*np.ones(num_particles)*u.uG # A constant field of 1.5 microgauss
cluster1.set_field("gas", "magnetic_field_x", B0, add=True)
If the field you are adding is a passive scalar, set passive_scalar=True:
import unyt as u
metals = 0.3*np.ones(num_particles)*u.Zsun
cluster1.set_field("gas", "metals", metals, passive_scalar=True)
Warning
It is obviously not recommended to alter a particle field created from a radial profile or an equilibrium condition!
ClusterParticles I/O#
ClusterParticles objects can be written
to disk or read from a file on disk. The normal way of writing the particles
to disk is to use the
write_particles() method:
# overwrite is a boolean which allows you to overwrite an existing file
parts.write_particles("my_particles.h5", overwrite=True)
A ClusterParticles object can be read
in from disk using the
from_file() method:
import cluster_generator as cg
new_parts = cg.ClusterParticles.from_file("my_particles.h5")
To only read in certain particle types from the file, specify them in
ptypes:
import cluster_generator as cg
# only gas particles
gas_only = cg.ClusterParticles.from_file("my_particles.h5", ptypes="gas")
# only dm, star particles
dm_star = cg.ClusterParticles.from_file("my_particles.h5",
ptypes=["dm", "star"])
Gadget-Like I/O#
cluster_generator also provides for the creation of Gadget-like snapshot/IC
files for use with codes such as Gadget, Arepo, GIZMO, etc. The
write_to_gadget_file()
writes an HDF5 file with the different particle types in the
ClusterParticles object in a format
that can be used as initial conditions for these codes. It requires a
box_size parameter, which determines the width of the cubical box that
the initial conditions will be set within.
box_size = 20000.0 # in kpc
parts.write_to_gadget_file("cluster_ics.hdf5", box_size, overwrite=True)
To create a new ClusterParticles object
from one of these files, use the
from_gadget_file() method:
import cluster_generator as cg
# all particle types
parts = cg.ClusterParticles.from_gadget_file("cluster_ics.hdf5")
# only gas particles
gas_only = cg.ClusterParticles.from_gadget_file("cluster_ics.hdf5",
ptypes="gas")
# only dm, star particles
dm_star = cg.ClusterParticles.from_gadget_file("cluster_ics.hdf5",
ptypes=["dm", "star"])
For more information on how these files are used in Gadget-like codes, see Simulation Software.